4. О ряде натуральных чисел

 

1

 

О том, что мир вокруг нас не совсем такой, каким он представляется нашему восприятию, догадывались уже давно. Еще Платон считал, что материальная действительность является лишь несовершенным отражением истинной жизни, сосредоточенной в бессмертных образах-идеях. В дальнейшем подобные догадки высказывали многие философы и ученые, начиная с немецкого математика Готфрида фон Лейбница и заканчивая нашим современником, физиком-теоретиком Давидом Бомом, автором фундаментальных работ по теории относительности и квантовой механике.

 

Так, согласно теории Бома, явления, которые мы воспринимаем органами чувств или при помощи приборов как дискретные, представляют лишь фрагмент реальности, так называемый эксплицитный или развернутый порядок. Но под этим развернутым порядком дискретных явлений находится скрытый или имплицитный порядок неразделимой целостности. И именно этот порядок неразделимой целостности и определяет нашу действительность. Иными словами, физические объекты только кажутся разделенными в пространстве и времени. На самом же деле они объединены неким основополагающим способом, а вселенная напоминает организм, отдельные клетки которого имеют смысл только в их отношении к целому.

 

Таким образом, выводы, к которым мы пришли в конце предыдущего раздела, не являются чем-то абсолютно новым. Новым, то есть тем, что пока еще никем не предпринималось, является наша попытка, во-первых, определить, что представляет собой сама неразделимая целостность и, во-вторых, построить конкретный механизм, способный наглядно показать, как именно эта целостность создает материальный мир дискретных явлений. Конечно, в нашем распоряжении нет оборудования, необходимого для проведения исследований в области субатомного мира. Не будем мы строить и математические модели этого мира, которые мало что могут нам объяснить. А попробуем решить проблему методом простых рассуждений, опираясь на самоочевидные и хорошо известные факты.

 

2

 

Итак, чтобы выяснить, что представляет собой неизвестная нам реальность, вначале надо подумать над тем, как вос­становить механизм возникновения образа. Тогда мы смогли бы по­нять, на каком этапе и как эта реальность фор­мирует образ.

 

Рассмотрим для этой цели механизм действия одного из органов чувств. И поскольку свыше 90 % получаемой информации приходится на зрение, ос­тановимся именно на зрении. Начнем с того, что воспри­ятие мира в фор­мах возможно лишь постольку, поскольку возможно восприятие цветов в их раздельности. В самом деле, чтобы обозначить границу ме­жду двумя предметами, надо иметь по крайней мере два цвета, в кото­рые эти пред­меты были бы окрашены. Ведь даже если мы видим их черно-белыми, они все равно имеют оттенки, позво­ляющие глазу отли­чать их друг от друга. Если бы мир был окрашен в один цвет, воспри­нимать его мы бы не смогли.

 

Но для начала видения одних границ между цветовыми полями мало: они уходят в бесконечность и не могут дать определенность, не­обходимую для создания формы. Такую определенность может дать только некий про­стейший объект, который являлся бы первым актом восприятия и с кото­рого мозг мог бы начать строительство формы. Та­ким простейшим объек­том может быть только точка, потому что проще точки ничего не бывает. Однако сама по себе точка воспринимаема быть не может: она может образоваться только в результате пере­сече­ния двух линий. Поэтому, чтобы точка была воспри­нимаема зрением, необходимо как минимум три цвета: два гранича­щих цвета дадут линию, протяжен­ную в обе сто­роны до беско­нечности, а третий цвет – ог­раничит эту линию другой линией (см. рисунок 6).

Но для формирования образа точки тоже недостаточно. По­скольку точка, как известно, длительности не имеет, сколько бы точек мы ни скла­ды­вали, в итоге, кроме точки, все равно ничего не полу­чится. Поэтому, чтобы возник образ, мозг должен сначала из совокуп­ности точек создать форму и только потом уже из совокупности форм, как из кирпичей, вы­строить образ. Причем, если учесть, что человече­ский мозг работает по принципу экономии энергии, форма эта должна быть простейшей, то есть для ее создания мозг должен ограничиваться минимально необходимой информацией. Такой про­стейшей формой может быть только треугольник, поскольку, чтобы его уви­деть, выде­лив из окружающего фона, мозг должен получить от зрения инфор­ма­цию всего о трех точках. Посмотрим, как на основании информации о трех точках мозг формирует треугольник. Возьмем три произвольно расположенные точки, каж­дая из которых ограничена тремя цвето­выми полями (см. рисунок 7).

                                        

 

Обра­тим внимание, что все они суще­ствуют самостоя­тельно и ничем друг с дру­гом не свя­заны. Чтобы мозг мог объеди­нить их в не­что единое, нужно, чтобы все они имели между со­бой что-то об­щее, что-то их объединяю­щее. Мы видим, что разде­ляют точки друг от друга цветовые поля. Пока каждая точка имеет по три ограничивающих ее поля, все они остаются полностью ав­то­номными. Значит, чтобы объединить эти три точки в тре­угольник, нужно цветовые поля всех трех точек организовать таким об­разом, чтобы каж­дая из них имела только по два своих поля, третье же было бы для них общим. То­гда возникшие между граничащими цвето­выми полями ли­нии и об­ра­зуют искомый треугольник.

 

Нетрудно сосчитать, что в этом случае, если каждая из трех точек бу­дет иметь только по два своих поля, а третье поле у них будет одно на всех, – ко­личество ограничивающих точки цветовых полей в сумме будет равно семи. Вот это и есть тот цветовой спектр, который воспри­нимается нашим зрением. Но каждая точка, как мы выяснили, имеет по три цветовых поля, а три точки в сумме будут иметь их уже девять. Куда же делись два цветовых поля?

 

Ответ может быть только один: мозг в целях придания воспри­ятиям формы просто «жертвует» их частью. Он как бы «делает вид», что этих цвето­вых полей не существует, отправляя их в область невос­принимае­мого. Из этого следует, что органами чувств человек воспри­нимает не семь, а девять цветов спектра, и тот факт, что человеческий мозг воспринимает лишь семь из них, говорит о том, что именно здесь и заложена причина из­менения реально­сти.

 

Любопытно, что еще Платон в знаменитом своем диалоге «Ти­мей» утверждал, что поверхность тел бог сотворил из треугольников. По его словам, «…любая глубина должна быть ограничена природой поверхности, а всякая плоская поверхность состоит из треугольников». Разу­меется, не надо думать, что эти треугольники можно увидеть глазами, – ведь их бесконечное множество, а построение из них образов происхо­дит на уровне подсоз­нания.

  

3

 

Здесь следует обратить внимание на любопытное совпадение, ко­торое прямо-таки бросается в глаза: число цветовых полей, посту­паю­щих на сетчатку глаза, соответствует ряду натуральных чисел от «1» до «9». При­чем семь из них соответствует числу полей ви­димого спектра, а два – его не­видимой части. При этом заметим, что количе­ство звуков му­зыкального лада тоже равно семи, а в соответст­вии с так называемой сте­реохимической тео­рией числу «7» соответст­вует также и количество ос­новных запахов. Не ис­ключено, что и осяза­ние, и вкус подпадают под это правило с той лишь разни­цей, что они не дифферен­цированы сознанием в такой же степени, как зрение и слух. Случайно ли это? Не является ли ряд натуральных чисел отраже­нием нашей способности различать цвета и звуки?

 

Как из­вестно, числа не все­гда существовали исключительно для обслуживания на­ших потребностей в счете. Как сказано в энциклопедии «Мифы народов мира», в архаических культурах число и счет были священными сред­ствами ориентации во все­ленной, с их помощью воспроизводилась структура космоса и правила по­ведения в нем че­ловека. Пифагорейцы, например, считали, что мир есть число, китайский муд­рец ХIII века Чжай Шень утверждал, что следование числу дает знание всех вещей, а тамильский поэт VII века Аппар писал о Шиве, что «он – число и цифра для числа». Начало применения чисел в счетно-хозяйственных целях относится к более поздней стадии, когда члены числового ряда утра­тили свои божественные качества, а сам число­вой ряд стал однород­ным. Значит, воз­никновение числового ряда связано не с потребно­с­тями счета. С чем?

 

Обратим внимание: когда мы заняты созерцанием картин при­роды, то невольно ищем в них какой-то порядок, какую-то геометриче­скую органи­за­цию. Это особенно заметно в произведениях живописи, всегда имеющих чет­кую композицию. Не только на реалистических полот­нах, но и в картинах с абстрактным изображе­нием должен присутствовать некий ритм, без которого эти картины просто перестают быть произведе­ниями ис­кусства. Но природа, как из­вестно, геометрических форм не создает. Значит, художник сам наделяет изображаемый объект пропорциями, стремясь тем са­мым установить с ним гармонические отношения. Не по­тому ли, что наше восприятие, имея геометрическую организацию, само закладывает в сознание чело­века такое требование? Но тогда ситуация иде­альной гармонии между че­ловеком и внешним миром возможна лишь в том случае, если внеш­ний мир будет организован на основе идеальных гео­метрических фи­гур. Например, как мир современных горо­дов.

 

Нетрудно представить в таком случае, что должен был испытать наш далекий предок, впервые ощутив себя в мире, который стано­вился для него внешним. Скорее всего, это было чувство чудо­вищного диском­форта, когда все вокруг воспринималось как один сплошной хаос, без всякой надежды отыскать в нем хоть одну прямую линию. Вот здесь-то у человека и могла возникнуть психологическая потребность придать миру ту форму, ко­торая соответствовала бы фор­мам его восприятия. То есть вна­чале вывести эти формы в сознание и перенести их на бумагу (глину, пергамент), а затем на их ос­нове выстроить рядом с реальным ми­ром свой, человеческий.

 

Вероятно, так и появляются точка, линия и треугольник, а также те несколько про­стых истин, которые мы называем постулатами. Что же касается ряда нату­ральных чисел, то он, скорее всего, тоже возникает из элементов восприятия. Только од­нородных, таких, которые были бы общими и для точки, и для линии, и для треугольника. Такими однородными элементами вос­приятия являются, как мы уже устано­вили, цветовые поля. Поскольку геометрически эти поля выглядят как плоскости, то есть однородно, они-то, как видно, и должны были стать тем эквивалентом, который позволил человеку создать ряд натуральных чисел. Так линия, протя­женная в обе стороны до беско­нечности и потому неопреде­ленная, видимо, на­чинает ассоциироваться с числом «2» (разделяет два цветовых поля), точка – первая определенность, с чис­лом «3» (три цветовых поля), а треугольник – с числами «7» (вторая опре­деленность) и «9» (полнота). Ос­тальные числа могли возникнуть в результате их сочетания.

 

Теперь можно, комбинируя различные эле­менты, строить математические модели мира, а потом на основании этих моделей вносить в реальный мир свои коррективы. Так возникает воплощенный в числе порядок, олицетворяющий для человека искомую гармонию. И одно­временно появляются предпосылки для создания учения об идеальном мире, который может постигаться только при по­мощи математики и по от­ношению к которому материальный мир явля­ется всего лишь его несовер­шенным отпе­чатком.

  

4

 

Итак, мы пришли к выводу, согласно которому первые девять чисел натурального ряда возникли из потребности нашего мозга в создании эле­мен­тарной геометрической формы. Но здесь возникает проблема в определении статуса математики как науки. Если исходить из того, что ряд натуральных чисел – это основа всей математики, то получается, что математика не имеет к реальности никакого отношения. Скорее она представляет собой умозрительную схему того, как мозг, получив информацию от органов чувств, выстраивает из нее струк­туру созер­цаемых нами форм. Не отсюда ли таинственная вездесущность математики, позво­ляющая использовать ее в самых разных сферах знания: ведь любая информа­ция об­рабатывается мозгом по одной и той же схеме?

 

Однако с другой стороны, математика является безупречным инструментом исследования и описания физических явлений. Ее абстрактные идеи находят полное соответствие во внешнем мире и прекрасно согласуются с опытом. Эвклидова геометрия, гелиоцентрическая система Коперника и Кеплера, механика Галилея и Ньютона, электромагнетизм Максвелла, теория относительности Эйнштейна – все это математика.

 

Что же, в таком случае, пред­став­ляет собой мате­матика? Отражает ли она какую-то реальность или же целиком является свободным творе­нием че­ловеческого духа? Или, говоря словами Эйнштейна, «Почему возможно такое превосходное соответствие математики с реальными предметами, если сама она является произведением только человеческой мысли, не связанной ни с каким опытом?». (Все цитаты данного раздела приведены по книге Мориса Клайна «Математика. Поиск истины»).

 

Следует сказать, что в истории науки вопрос этот породил целую полемику, хотя все множество высказанных на этот счет мнений можно свести к двум основным. Согласно первому из них, «мир человеческого опыта есть по существу творение нашего разума и если бы мы только могли понять, как работает разум, нам удалось бы вывести всю физику, а быть может и все естествознание». Автором данного высказывания является Артур Эддингтон, но сходной точки зрения придерживались также и Кант, и Пуанкаре, и Эйнштейн. Причем, наиболее радикально данную позицию выразил в работе «Прагматизм» американский философ Уильям Джеймс. По его мнению, «Все грандиозные достижения математики и естественных наук… проистекают из нашего неутолимого желания придать миру в наших умах более рациональную форму, чем та, которую придал ему грубый порядок нашего опыта».

 

Однако, согласно другой точке зрения, математический порядок свойствен самой природе, а законы, выводимые нашим разумом, являются всего лишь отражением этого порядка. В числе наиболее известных ее сторонников можно назвать Вейля, Мостовски, Больцмана, Гельмгольца, Маха, Бриджмена и Планка. Как писал в книге «Философия математики и естественных наук» Герман Вейль, «В природе существует внутренне присущая ей скрытая гармония, отражающаяся в наших умах в виде простых математических законов. Именно этим объясняется, почему природные явления удается предсказывать с помощью комбинации наблюдений и математического анализа. Сверх всяких ожиданий убеждение (я бы лучше сказал, мечта!) в существовании гармонии в природе находит все новые и новые подтверждения в истории физики».

 

Такая разноголосица мнений существует по одной единственной причине: несмотря на очевидность связи между физическим миром и математическими структурами, вопрос о том, что это за связь, какими причинами она обусловлена, и по сей день остается без ответа. Как признался американский физик Фримен Дайсон, «мы, по-видимому, еще не приблизились к пониманию взаимосвязи между физическим и математическим мирами».

 

Кант полагал, что ответить на этот вопрос можно лишь в том случае, если станет понятно, как вообще возможна наука математика. Сам же он, как известно, считал, что «все­общие и необхо­димые законы опыта принадлежат не самой природе, а только разуму, ко­торый вкладывает их в природу». По мысли Канта, мы воспринимаем, органи­зуем и постигаем окружающую реальность не саму по себе, а только в соответствии с фор­мами, заложенными в нас природой. Сама же реальность остается для нас полностью недоступной и является, как он называл ее, «вещью в себе». Поэтому для Канта так и осталось загадкой, почему абстрактные математические истины находят соответствия во внешнем мире. 

 

Проблема, на мой взгляд, решается достаточно просто, если учесть, что механизм человеческого восприятия имеет два уровня. Кант думал, что формы, в ко­торых чело­век воспринимает мир, возни­кают вместе с ощущениями, поступающими из внешнего мира. На самом же деле эти формы воз­никают только на втором этапе воспри­ятия, в связи с появлением у че­ловека памяти (см. «Человек и его воспри­ятие», 5, 6). А ощущения, по­ступающие от ор­ганов чувств, явля­ются физиологи­ческими реакциями и, судя по всему, пере­дают поступаю­щий в организм сиг­нал неизме­ненным. Поэтому ощуще­ния являются непо­средственным отраже­нием той реальности, которую Кант считал непозна­ваемой. А поскольку ощущения получили свое от­ражение в ряде натураль­ных чисел, этот послед­ний является са­мой объ­ективной характеристикой этой реально­сти. Вот по­чему даже наиболее головокружительные матема­тические модели находят со­от­ветствия в ре­альных процессах.

 

5

 

Итак, ровно девять элементов восприятия потребовались на­шему мозгу, чтобы сконструировать простейшую геометрическую форму. Но ряд натуральных чисел не ограничивается числом «9». Попробуем выяснить, для какой цели нашему мозгу могли потребоваться числа от «10» и выше?

 

Существует точка зрения, что числа натурального ряда, увеличиваясь каждый раз на одну единицу, уходят в «дурную» беско­нечность. Я пола­гаю, эта точка зрения в корне ошибочна. Чтобы в этом убе­диться, рассмот­рим па­радокс так называемых трансфинитных чисел. Суть его заключается в сле­дующем. Если взять два ряда целых чисел от 1 до 10, один из которых содер­жал бы в себе все числа без исключения, а второй только четные, то во втором ряду количество чисел будет в два раза меньше, чем в первом:

 

                                   1, 2, 3, 4, 5, 6, 7, 8, 9, 10

 

                                            2, 4, 6, 8, 10       

 

Казалось бы, число целых чисел всегда должно быть больше, чем число четных. Но если взять два ряда чисел, один из которых будет ря­дом целых, а другой рядом четных чисел, и продолжить их до беско­нечности, то окажется, что как бы долго мы их ни продолжали, каж­дому числу од­ного ряда будет со­ответствовать число в другом ряду. То есть их количе­ство будет одинаковым:

 

                   1, 2, 3, 4, 5, 6…

                                          2, 4, 6, 8, 10, 12…

 

В свое время Лейбниц, обративший внимание на это обстоятель­ство, счел его противоречием. Однако приведенный факт свидетельст­вовал бы о противоречии лишь в том случае, если бы каждое новое число действи­тельно было больше предыдущего. На самом деле это не так. Числа «11», «12», «254», «12142» и т.д. представляют собой не что иное, как тот же ряд простых чисел, те же «1», «2», «3», только не­сколько видоизмененных. В самом деле, число «10», следующее после «9», начинает заново ряд про­стых чисел, потому что 10=1+0=1. Далее, 11=1+1=2; 12=1+2=3 и т.д. Таким образом, можно со­ставить следую­щую таблицу (см. таблицу 1).

 

                                                                                              Таблица 1

 

1, 2, 3, 4, 5, 6, 7, 8, 9,.......................................………………..

10(1), 11(2), 12(3), 13(4), 14(5), 15(6), 16(7), 17(8), 18(9),.....

19(1), 20(2), 21(3), 22(4), 23(5), 24(6), 25(7), 26(8), 27(9),.....

28(1),...................................................…………………………

..............................................…………………………99(9),.....

100(1), 101(2), 102(3),....................................…………………

.............................................…………………………999(9),....

.........................................................……………………………

1234(1), 1235(2), 1236(3), и т.д.

 

Что же означают многозначные числа в реальности? Я думаю, много­значность числа свидетельствует о том, что каждое простое число имеет структурное строение и любая его часть, подчиняясь общему по­рядку, за­ни­мает в нем строго определенное место. Например, число «11» не озна­чает, что оно больше числа «10» на одну единицу, а оно означает, что в не­кой форме, которая выражается числом «10=1+0=1», она занимает фраг­мент реальности, состоящий из «1» и еще одной «1». Другими словами, ряд натуральных чисел продолжается не в «дурную бесконечность», как об этом принято думать, а в глубину структуры. Если же структура неисчер­паема, парадокса трансфинит­ных чисел не существует, так как любое число является только характеристикой од­ного из ее фрагментов.

 

Но, если число отражает деятельность мозга по образованию тре­угольников как простейших строительных форм, из которых должен соз­да­ваться образ, и при этом само имеет структурное строение, это может озна­чать только одно: своей структурой число показывает, в ка­ком порядке мозг должен расположить треугольники, чтобы получить зримый образ.

 

Нет оснований сомневаться, что алгоритм структурирования тре­угольников ничем не отличается от алгоритма их образования из сово­куп­ности цветовых полей. То есть сначала три элемента рождают чет­вер­тый (как три цвета – точку); потом три новых элемента рождают следую­щий (три точки – треугольник), в который входит уже девять первоначаль­ных элементов; по­том объединяются три фигуры, состоя­щие уже из 27 элементов, и т.д. В итоге вся форма оказывается струк­турирована таким образом, что каждая ее часть становится некой еди­ницей в системе троич­ности, которая тоже является еди­ницей в системе троичности, а эта, новая система – тоже единица, и так до бесконечно­сти. В качестве наглядного пособия для описания данной структуры я пред­ложил бы так называемый «Круг универсума», из трактата «О предпо­ложениях» Николая Кузанского (см. рису­нок 8). Благодаря этой нехитрой схеме можно легко вычислить, какую структуру отражает то или иное число.

 

В Круг вписаны 3 большие окружности, в каждую из которых впи­саны по 3 средние, а в каждую среднюю окружность, в свою оче­редь, впи­саны 3 ма­лые. Таким образом, получается, что каж­дая боль­шая окружность содержит по 3 средних и по 9 малых. Всего, если счи­тать вместе с Кругом, – 40 окруж­ностей. Это и есть структура любого числа до 40. Единицам здесь соответст­вует количество средних окруж­ностей, десяткам – количе­ство больших. Чтобы определить, из каких элементов состоит то или иное число, нужно к числу окружно­стей, от­ражающих десятки, прибавить число окружностей, отра­жающих еди­ницы. Например, структура числа 29 будет состоять из 2 больших эле­ментов и 9 средних. Но 2 больших элемента включают в себя 18 ма­лых. Поэтому полная структура числа 29 будет со­стоять из 2 больших эле­ментов, 18 малых и 9 средних. Если же проделать подобную опера­цию с каждым двузначным числом до 40, можно получить структуру лю­бого числа до 40 (см. таблицу 2).

 

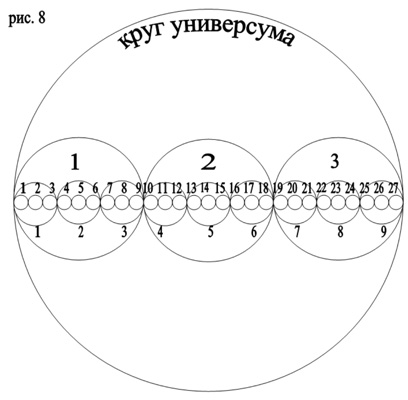
                                                                                  Таблица 2

            10(1) =  (1 + 0) + 9

            11(2) =  (1 + 1) + 9

            12(3) =  (1 + 2) + 9

            13(4) =  (1 + 3) + 9

            14(5) =  (1 + 4) + 9

            15(6) =  (1 + 5) + 9

            16(7) =  (1 + 6) + 9

            17(8) =  (1 + 7) + 9

            18(9) =  (1 + 8) + 9

            19(1) =  (1 + 9) + 9

            20(2) =  (2 + 0) + 18

            21(3) =  (2 + 1) + 18

            22(4) =  (2 + 2) + 18

            23(5) =  (2 + 3) + 18

            24(6) =  (2 + 4) + 18

            25(7) =  (2 + 5) + 18

            26(8) =  (2 + 6) + 18

            27(9) =  (2 + 7) + 18

            28(1) =  (2 + 8) + 18

            29(2) =  (2 + 9) + 18

            30(3) =  (3 + 0) + 18

            31(4) =  (3 + 1) + 27

            32(5) =  (3 + 2) + 27

            33(6) =  (3 + 3) + 27

            34(7) =  (3 + 4) + 27

            35(8) =  (3 + 5) + 27

            36(9) =  (3 + 6) + 27

            37(1) =  (3 + 7) + 27

            38(2) =  (3 + 8) + 27

            39(3) =  (3 + 9) + 27

Как видим, любое двухзначное число отличается от соответст­вую­щего ему простого тем, что состоит из суммы двух чисел. Причем одно из этих чисел состоит из единиц, каждая из которых включает в себя струк­туру из 9 элементов. Но любое простое число тоже может быть представлено в виде суммы единиц, каждая из которых имеет струк­туру, состоящую из 9 элементов. По­этому, если учесть, что ка­ждая входящая в двузначное число единица имеет структурное строение, можно констати­ровать, что структуры любых соответствующих друг другу чисел между со­бой подобны.

 

Следует добавить, что, если исходное число будет больше 40, можно определить его структуру, составив новый Круг универсума, который объе­динил бы в себе три круга по 40 окружностей. Так же можно составить подобный Круг для определе­ния строения любого много­значного числа, что, на мой взгляд, говорит о глубинной связи, существую­щей между бесконечностью числового ряда и неисчерпаемостью струк­туры.

 

                                                           6

 

Итак, мы выяснили, каким способом мозг формирует об­раз: сначала из ощущений он строит элементарную гео­метрическую форму, а потом, группируя в определенном порядке бес­численное мно­же­ство таких форм, получает образ. При этом часть ощущений, не­су­щих ин­формацию о реальности, утрачивается. Но надо помнить, что в составлении образа участ­вуют два фактора – линия и число: линия соз­дает форму, а число выстраивает из совокупности форм структуру об­раза. Информация утрачивается именно при созда­нии форм. Что же ка­сается структуры об­раза, она воспринимается не­посредственно через ощущения, поэтому соот­ветствует отраженной в числе структуре ре­альности. Таким образом, хотя сам облик реальности и продолжает ос­таваться неизвестным, ее структура получает в ряде на­тураль­ных чисел свое полное отражение.

 

Если сказанное верно, любой процесс во вселенной может быть упо­доблен числовому ряду. А это означает, что аналогично тому, как в чи­словом ряде происходит повторение одних и тех же простых чисел, только обла­дающих более сложной структурой, так и в реально­сти можно наблю­дать пе­риодическую повторяемость качеств, которые  ранее проявлялись в большей простоте.

 

Чтобы проверить верность наших предположений, возьмем пе­риоди­че­скую систему элементов Менделеева. Можно убедиться, что изменение свойств элементов в соответствии с увеличением заряда ядра атома на одну единицу происходят только до определенного пре­дела, а именно до числа «9». А дальше они начинают периодически по­вто­ряться. Например, свой­ства магния, имеющего порядковый номер 12 (1+2=3), повторяют свойства цинка – порядковый номер 30 (3+0=3), а заодно и кадмия – 48 (4+8=12=1+2=3). Свойства аргона 18 (1+8=9) повторяют свойства криптона 36 (3+6=9) и ксенона 54 (5+4=9). Ана­ло­гично повторяются свой­ства в цепочке элемен­тов – сера, селен, теллур, имеющих порядковые номера, соот­ветственно, – 16 (1+6=7), 34 (3+4=7) и 52 (5+2=7), а также калий, ру­бидий, цезий – 19, 37, 55, кальций, стронций, барий – 20, 38, 56.

 

В свое время, чтобы найти причину периодической повторяемо­сти свойств элементов на фоне неизменности роста заряда атомного ядра, было воздвигнуто такое грандиозное сооружение, как ядерная фи­зика. Была при­думана сложнейшая система электронных орбит, обла­дающих множеством характеристик (квантовых чисел). Сейчас ясно, что свойства элементов зависят от структуры той сущности, кото­рая лежит в основе реального мира и соответствует структуре число­вого ряда. Значит, число­вой ряд является первой в мире моделью мироздания, где зашиф­рована его структура, воспринимаемая человеком при помощи пяти органов чувств.

 

Замечательно, что люди издавна чувствовали ритмический харак­тер мироздания. Вот почему монада, или единица, всегда символизиро­вала мо­нолит, «Бога истинного и Отца всего», как сказано в апокрифе Иоанна. Триада, или тройка, – полное равновесие монады и диады, где единица есть Бог Отец, двойка – Бог Мать, а тройка – Бог Сын (а еще это три богатыря, три члена социальной группы и троичный принцип композиции в произве­дениях искусства – трилогии, триптихи, терцины, вплоть до трилистников «Кипари­сового ларца» у Иннокентия Аннен­ского). Что же касается числа девять, то в старой китайской традиции оно используется в значении «все».

 

Наверное, неслучайно число 64 (единица), которому соответст­вует ко­личество кодовых слов, или кодонов, в носительнице генетиче­ского кода – молекуле ДНК, одновременно соответствует и количеству гексаграмм в ки­тайской классической «Книге Перемен» и количеству клеток на шахмат­ной доске. 64 кодона молекулы ДНК укладываются без остатка в 19 витков ее двойной спирали. Если учесть, что число 19 соответствует 19 годам так на­зываемого Ментонового цикла, лежащего в основании греческого кален­даря, можно предположить, что состоя­щий из 19 лет временной цикл пред­ставляет генетическую программу, за время выполнения которой человече­ство отра­батывает все преду­смотренные в ней варианты, после чего цикл повторяется (Дюла Хар­нади). Но тогда «Книгу Перемен», как и игру в шахматы можно рассматривать как модели этого процесса, поскольку 64 клетки шахматной доски, как и 64 гексаграммы «Книги Перемен», тоже ох­ватывают все возможные варианты любой си­туации.

 

Любопытно, что соответствие числа его внутренней сути наблю­да­ется и в таком феномене, как временные циклы. Это и четыре индус­ских «Юги» (1728000; 1296000; 864000; 432000 лет), и период зодиа­кального смещения, равный 2160 лет, и прецессия, в течение кото­рой происходит один полный оборот земной оси. Все они со­ответствуют числу 9, то есть полноте. И это понятно, потому что заверше­ние каждого из таких циклов знаменуется наступ­лением коренных измене­ний в мироздании. Так, согласно индийской периодизации, четыре юги составляют одну махаюгу, а тысяча махаюг, повторяющихся друг за другом, – одну кальпу, или один день Брахмы. В конце каждой кальпы на небе появляются двенадцать Солнц, и они дотла сжигают миры, возрождающиеся затем в новой кальпе.

 

7

 

Но что же представляет собой мир, в котором мы живем и ча­стью которого являемся? Что это за субстанция, зрительное восприятие ко­торой возможно лишь поскольку возможно восприятие цветов в их раз­дельности? «Цвет…, – сказал как-то Николай Кузанский, – пребы­вает в свете не как в ином, а как в своем начале, потому что цвет есть лишь предел света в про­зрачной среде...». Поскольку объективно свет – это электромагнитные волны, допустимо предположить, что все види­мое, слышимое и ощущае­мое нами представляет собой своеобразный энер­гетический континуум, не­кое силовое поле, которое воспринима­ется зрением как цвет, слухом – как звук, а осяза­нием – как вещество. При­чем, образующей и организующей основой этого поля мы будем счи­тать расталкивающую силу.

 

Напомню, что понятие расталкивающей силы было введено нами взамен концепции Большого Взрыва, чтобы устранить противоре­чие, связанное со вторым началом термодинамики (см. «Пространство, ве­щество и время», 1). Мы предположили тогда, что расталкивающая сила исходит из единого цен­тра (его мы назвали полюсом гравитации) и порождает силу гравита­ции, яв­ляющуюся реакцией на расталкивающую силу и направленную в сторону, ей противополож­ную. Тогда же мы предприняли попытку выяс­нить, как под воздейст­вием расталкивающей силы могли образоваться про­странство, веще­ство и время. Однако потом мы выяснили, что про­странство, вещество и время реаль­ности не отра­жают, поскольку являются только формами нашего воспри­ятия. Поэтому сейчас настало время ввести в нашу пер­вую модель коррективы и уточнить, что под воз­дей­ствием рас­талки­вающей силы возни­кают не пространство, вещество и время, а не­кая, пока еще не известная нам структура, ко­торая вос­при­нимает саму себя в формах про­странства, вещества и вре­мени.

 

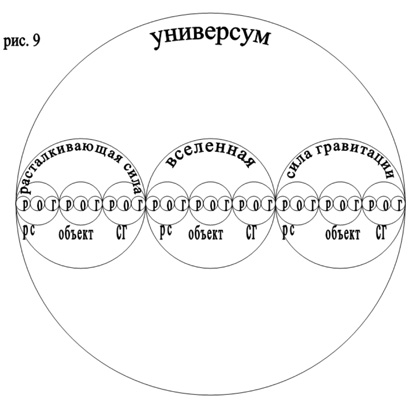
Посмот­рим, что может представлять собой эта структура. Обра­тимся вновь к «Кругу универсума», так как именно эта схема отражает ее наибо­лее наглядно. Начнем с самого большого круга, сим­волизи­рующего весь наш мир или, лучше сказать, универсум, по­скольку к данному контексту этот термин подходит в гораздо большей степени. Как видим, Круг вклю­чает в себя три окружности – две край­ние и сред­нюю. Мы предположили, что все­ленная, символом которой является Круг, возникла в результате взаимодей­ствия двух сил – рас­талкиваю­щей и гравитационной. Нетрудно догадаться, что одна из крайних ок­ружностей олицетворяет собой растал­кивающую силу, дру­гая крайняя – силу гравитации, а центральная – мате­риальную вселен­ную как ре­зультат их взаимодействия. 

 

 

Таким образом, три окружности, включенные в первый круг, пред­ставляют собой триединство из расталкивающей силы, силы гра­витации и вселенной. Но каждая из этих больших окружностей в свою очередь тоже включает в себя по три окружности, и каждая из этих окружностей опять включают в себя по три окружности, и так до бесконечности (см. рисунок 9). Значит, все вписанные в Круг универсума окружности представляют собой такие же триединства, ка­ждое из которых состоит из расталки­вающей силы, силы гравитации и не­коего объекта, величина и значение которого зависят от величины и зна­чения порождающих его сил. В це­лом же вселенная организована таким обра­зом, что все ее устройство от­ражается в каждом, даже самом малом фраг­менте поля, а любой самый малый фрагмент поля во всей полноте содер­жит в себе вселен­ную. Теперь понятно, почему законы математики, выведенные из наблюдений за процессами, происходящими в макромире, оказываются действенными и в мире атома: и вселенная, и атом имеют одну и ту же структуру.

      

Примечательно, что похожая картина является содержанием не­которых древних текстов. Так, согласно легенде, известной в тради­циях древнекитай­ской буддистской школы хуаянь, императрица Ву, оказав­шись не в состоя­нии понять сложности хуаяньской философии, попро­сила од­ного из основа­телей школы Фа Цанга объяснить ей на по­нятном примере принципы косми­ческой взаимозависимости. Фа Цанг выбрал во дворце ус­тавленную зерка­лами комнату, подвесил к ее по­толку го­рящий светильник, а затем поместил в центре комнаты малень­кий кри­сталл. Когда императ­рица Ву увидела, что все окружающее от­ражается в кристалле так же, как и кри­сталл отражается во всем окру­жающем, она поняла, как получается, что в Предельной Реаль­ности бесконечно малое содержит бесконечно большое, а бесконечно боль­шое – беско­нечно малое (С. Гроф).

 

Чтобы в полной мере осознать разницу между нынешней нашей мо­де­лью и той, которую мы построили на основании современной фи­зиче­ской картины мира, нужно понять, почему понятия, которые иг­рают основополагающую роль в теории относительности, не подходят в качестве фундаментальных для квантовой меха­ники. Дело в том, что теория относи­тельности, как из­вестно, описывает физическую реаль­ность в терми­нах про­странства и времени. В квантовой же механике ни про­странства, ни времени нет. Там есть волна, то есть вибрация, которая суще­ствует вне про­странства и времени и которую характеризуют такие понятия, как частота и длина волны.

 

Но мир, где есть пространство и время – это мир на­ших вос­приятий, а мир вибраций, как мы установили, – это, если вос­пользо­ваться термином Канта, «вещь в себе», которая для восприятия недос­тупна. По­этому теорию относительности можно рассмат­ри­вать как  метафору квантовой механики, а квантово-механический, волно­вой мир – как мир ис­тинной реальности, о характере которого можно су­дить только с той или иной степенью вероятности. В данной связи уме­стно вспомнить так называе­мый «Миф о пещере», изложен­ный Плато­ном в VII книге его «Государства». Там, как известно, при­кованные от рождения ли­цом к стене люди обречены всю жизнь созер­цать лишь тени предметов, в то время как сами они непоко­лебимо убе­ждены, что эти тени и есть на­стоящие предметы.

 

8

 

Следует заметить, что в нынешней нашей модели функции всех со­став­ляющих прежней модели должны измениться самым коренным обра­зом. Ранее, в соответствии с теорией Большого Взрыва, мы пред­ставляли себе центр вселенной исключительно в про­странственном смысле. И поскольку пространственный центр у вселенной мог быть только одним, соот­ветственно одной могла быть и исходящая из него растал­кивающая сила, и порожденная ею сила гравитации. Поэтому понять, как это единооб­разное действие расталкивающей силы приво­дит к су­щест­вующему многооб­разию форм, в рамках той сис­темы не представ­лялось возмож­ным.

 

Теперь же оказалось, что вселенная представляет со­бой энергети­ческое поле, а это значит, что каждый фрагмент этого поля имеет свою растал­ки­ваю­щую силу, свою силу гра­витации и свой полюс грави­та­ции. Так, любое космическое тело получает при­сущую ему шаровидную форму именно по­тому, что формируется под воздействием своей расталки­ваю­щей силы и своей силы гравитации. В свою очередь каждая система космических тел (солнечная система или галактика), тоже имеет форму либо шара, либо диска, либо спирали. А это значит, что и каждая система космических тел формируется под воздействием своей растал­кивающей силы и свей силы грави­тации. И, наконец, венцом всей конструкции является вселенная, имеющая такую же шаровидную форму, как и все входящие в ее состав объекты. Что же касается по­люса грави­та­ции, то у каждого космического образования он свой: у звезд и пла­нет – ядро, у галактики и вселенной – «черная дыра». То есть, можно сказать, что ранее получен­ная нами модель вселенной (см. «Пространство, вещество и время») оказывается частным слу­чаем всеобщей модели универсума.

 

Можно предположить, что образование каждой кон­крет­ной формы и их от­ли­чие друг от друга обусловлено положе­нием, ко­то­рое эти фраг­менты за­ни­мают в целом. По­скольку в энергетическом континууме напряжен­ность поля, по мере удаления от источника энергии, должна изме­няться, а вся­кий фраг­мент поля яв­ляется закон­ченной энергетической фор­мой, энер­гетиче­ский по­тен­циал этих форм по мере удаления от ис­точ­ника энергии тоже дол­жен изме­няться. Так, в за­висимости от положе­ния в це­лом, в каждой точке уни­версума происходит образо­вание своеобраз­ных энерге­тиче­ских форм или матриц, которые и становятся обра­зующими либо для атомов, либо для рас­тений, либо для животных.

 

Что же касается самого процесса формообразования, то он, судя по всему, обусловлен действием единого для универсума закона, кото­рый проявляет себя в виде взаимодей­ствия между расталкивающей си­лой и силой гравитации, и выража­ется, как мы сейчас увидим, от­ноше­нием золотого сече­ния.

 

На­помню: золотое сечение – это геомет­риче­ская прогрессия, ка­ж­дый но­вый член которой является ре­зульта­том ум­ножения предыду­щего члена на число 1,618 (или на 0,618, если про­грессия убывающая). Главной осо­бенно­стью этого сечения яв­ляется его связь со строением живых форм. Ко­личество процессов, по­рядок кото­рых выражается от­ноше­нием золо­того сечения, по­истине не­исчис­лимо. По этому закону проис­ходит раз­множение видов, рас­преде­ление ли­ствы на ветвях де­ревьев, закручива­ние спиралей на дисках подсолну­хов. Даже пропор­ции чело­веческого тела тоже свя­заны отно­шением зо­ло­того сечения. Так, если расстояние от пупка до ма­кушки принять за единицу, то рас­стояние от пупка до стопы будет равна – 1,618, а полная высота фигуры составит 2,618 или 1,618 2.  

 

Долгое время причины столь широкого распространения этого фено­мена были неясны. Но в 1986 году вышла книга костромского ар­хитектора И. Шевелева «Принцип пропорции». В ней на основа­нии несложных математических построений было неос­поримо доказано, что от­ношение золотого сечения имеет непо­средственную связь с геомет­рией сферы. Сама же сфера возникает как результат взаимодействия двух противоположно направленных сил: с одной стороны, это энергия роста жи­вого объекта, а с другой – некая внешняя сила, которую автор счи­тал силой притяжения Земли.

 

В результате анализа их взаимодействий Шевелевым было полу­чено несколько универсальных кривых, которым в природе соответст­вуют бес­численное множество интерпретаций. Это кривые типа «яб­локо» и «яйцо», из которых природа создает затем и раковину моллю­ска, и скорлупу яйца, и мозговую часть черепа, а также другие формы, пред­назначенные для ох­раны самых важных и беззащитных частей ор­ганизма. Так стала понятна зависи­мость между действующими в при­роде силами и формами объектов.

 

Для нас же в исследовании костром­ского архитектора важно то, что в энергии роста живого объ­екта мы узнаем расталкивающую силу, а в силе притяжения Земли – силу гравитации. Таким образом, можно кон­статировать, что все суще­ствующие в природе формы образуются в ре­зуль­тате действия единого закона, в основе которого лежит отношение ме­жду расталкивающей силой и силой гравитации, равное отношению золотого сечения.

 

И тут мы подходим к главному выводу данного раздела. Он состоит в том, что, поскольку один и тот же закон является образующим и для организма, и для вселен­ной, ничто не мешает нам сделать вывод, что вселенная в целом, как и лю­бой ее фрагмент, является живым организмом, а обра­зующий ее закон – единым для вселенной законом, представляющим ее генетический код.

 

Следует обра­тить вни­мание, что ка­ждая образующая тот или иной кон­кретный орга­низм матрица является, с одной стороны, ав­то­номным це­лым, а с дру­гой – частью дру­гого целого, от­носящегося к более высо­кому уровню. Поэтому структура поля организована таким образом, что со­вокупность организмов каждого уровня составляет ор­ганизм бо­лее вы­сокого уровня, в котором другие ор­ганизмы пребывают в ка­че­стве его отдель­ных органов. Так совокупность индивидов со­ставляет кол­лективы особей (рой, стая, стадо и т.д.), а коллективы особей размещаются в живой экологической системе, которую тоже можно расценивать как организм следующего уровня.

 

9

 

Необходимо различать, по-видимому, энергетическую форму, или матрицу, где происходит зарождение организма, от самого орга­низма. Энер­гетическая матрица представляет собой энергетический по­тенциал вселен­ной, ее генетическую программу или, если воспользоваться термином Платона, ее идею. Поэтому матрица не подвержена из­менению. Она содержит в себе прошлое, настоящее и бу­дущее в единовре­менно­сти и пребывает фактически в том состоянии, которое мы называем вечностью.

 

Организм является инструментом реализации программы. Возни­кает он так же, как в физической модели возникает вещество (см. «Про­странство, вещество и время», 3), то есть в результате взаимодействия двух сил – рас­талкивающей и гравитационной. Но, в отличие от физи­че­ской модели, где форма вещества остается неопределенной, веще­ство, со­ставляющее организм наполняет конкрет­ную форму, поэтому ста­но­вится конкретным организмом.

 

В ре­зуль­тате воз­действия силы гравитации организм дрей­фует к своему по­люсу гра­ви­тации, по пути излучая, то есть теряя часть энер­гии. По­теря энергии воспринимается им как смена внутренних со­стояний и угроза жизни: если уровень внутрен­ней энер­гии ор­ганизма выходит за рамки уровня энергии мат­рицы, ор­га­низм по­ги­бает, так как оказывается на энергети­ческом уровне, соот­вет­ствую­щем по­ложению другого орга­низма. На практике это оз­начает, что про­стой ор­ганизм может пребы­вать лишь в той среде, к ко­то­рой он при­способ­лен – птица в воздухе, рыба в воде, дож­девой червь в земле, по­скольку в энергети­ческом поле воздух, вода и земля как раз и пред­став­ляют со­бой его раз­ные энерге­тические уровни.

 

Напротив, расталкивающая сила проявляет себя в виде стремле­ния организма к восстановлению своей внутренней энергии за счет по­глоще­ния других организмов, а значит, и других энергий. Процесс на­полнения веществом, и, следовательно, энергией формы, представляет собой процесс станов­ления и явля­ется спосо­бом реализации программы. Таким образом, задача организма как становящегося объекта заключается в восстановления энергии, утраченной в результате его дрейфа к полюсу гравитации и под­держании уровня внутренней энергии на уровне энер­гии мат­рицы.

 

Поскольку ут­рата энергии, наступающая в результате дрейфа организма к полюсу гравитации, воспринимается им как смена внутренних состояний, а сам дрейф мы определили как время (см. «Пространство, вещество, время», 6), значит, смена внутрен­них состоя­ний для организма является временем. А из этого следует, что в отличие от матрицы, которая пребывает в состоянии вечности, процесс становления протекает во времени. Причем, процесс этот продолжается до тех пор, пока в ходе своего дрейфа под воздействием силы гравитации орга­низм не дости­гает по­люса гравита­ции. Тогда становление прекра­ща­ется, насту­пает ги­бель организма, а на осво­бо­дившемся в матрице месте на­чи­нается ста­новле­ние нового орга­низма. 

 

Так матрица не просто порождает один организм за другим, а ка­ждый раз порождает один и тот же организм. Как заметил Шопенгауэр, «удел львов требует львиности, которая во времени предстает как не­кий бес­смертный лев, живущий за счет непрестанно воспроизводя­щихся индиви­дов; их рожде­ние и смерть не что иное, как биение пульса этого непрехо­дящего льва». По­хоже, в нашей версии эта точка зрения получила свое под­тверждение.

 

Разумеется, следует иметь в виду, что процесс этот происходит не только на уровне индивидов, но на всех уровнях энерге­тиче­ской пирамиды, начиная с субатомных частиц и заканчивая универсумом в целом. В результате каждая живая система, включая и универсум, переживает периоды своего возникновения, становления и гибели. А это значит, что все входящие в универсум живые системы пребывают в состоянии постоянного изменения, обеспечивая, тем самым, изменение условий существования для живых систем более низких уровней. Отсюда и мутации, которые приводят к изменению морфологии организмов и появлению новых видов.

 

Таким образом, в отличие от теории эволюции, которая объясняет существующую в природе изменчивость биологических видов случайными мутациями, мы получили схему, в которой мутации являются целенаправленными. Их целенаправленность обеспечивается общей для универсума программой становления, в которую программы становления всех входящих в универсум живых систем являются составными частями этой единой программы.

 

Похожие статьи:

Газета → Абсолют (Опыт моделирования)

Газета → 1. Постановка задачи. Обоснование метода

Газета → КОФЕ. Рецепты приготовления

Газета → 3. Человек и его восприятие

Газета → 2. Пространство, вещество и время